Conceptos 2

Conceptos 2

Rotacional:

En el cálculo vectorial, el rotacional o rotor es un operador vectorial sobre campos vectoriales definidos en un abierto de que muestra la tendencia de un campo vectorial a inducir rotación alrededor de un punto.

Matemáticamente, esta idea se expresa como el límite de la circulación del campo vectorial, cuando la curva sobre la que se integra se reduce a un punto:

Aquí, es el área de la superficie apoyada en la curva , que se reduce a un punto. El resultado de este límite no es el rotacional completo (que es un vector), sino solo su componente según la dirección normal a  y orientada según la regla de la mano derecha. Para obtener el rotacional completo deberán calcularse tres límites, considerando tres curvas situadas en planos perpendiculares.

Aunque el que el rotacional de un campo alrededor de un punto sea distinto de cero no implica que las líneas de campo giren alrededor de ese punto y lo encierren. Por ejemplo, el campo de velocidades de un fluido que circula por una tubería (conocido como perfil de Poiseuille) posee un rotacional no nulo en todas partes, salvo en el eje central, pese a que la corriente fluye en línea recta: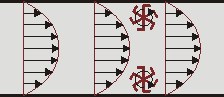

La idea es que si colocamos una rueda de paletas infinitamente pequeña en el interior del campo vectorial, esta rueda girará, aunque el campo tenga siempre la misma dirección, debido a la diferente magnitud del campo a un lado y a otro de la rueda.

Expresión en coordenadas cartesianas

Partiendo de la definición mediante un límite, puede demostrarse que la expresión, en coordenadas cartesianas, del rotacional es:

que se puede expresar de forma más concisa con ayuda del operador nabla como un producto vectorial, calculable mediante un determinante:

 

Debe tenerse muy presente que dicho determinante en realidad no es tal pues los elementos de la segunda fila no tienen argumento y por tanto carecen de sentido. Además dicho determinante sólo puede desarrollarse por la primera fila. En definitiva, la notación en forma de determinante sirve para recordar fácilmente la expresión del rotacional.

En la notación de Einstein, con el símbolo de Levi-Civita se escribe como:

Gradiente:

En análisis matemático (cálculo avanzado), particularmente en análisis vectorial, el gradiente o también conocido como vector gradiente, denotado de un campo escalar es un campo vectorial. El vector gradiente de evaluado en un punto genérico del dominio de , (), indica la dirección en la cual el campo varía más rápidamente y su módulo representa el ritmo de variación de en la dirección de dicho vector gradiente. El gradiente se representa con el operador diferencial nabla seguido de la función (atención a no confundir el gradiente con la divergencia, esta última se denota con un punto de producto escalar entre el operador nabla y el campo). También puede representarse mediante , o usando la notación  . La generalización del concepto de gradiente a campos  vectoriales es el concepto de matriz Jacobiana.

Se toma como campo escalar el que se asigna a cada punto del espacio una presión P (campo escalar de 3 variables), entonces el vector gradiente en un punto genérico del espacio indicará la dirección en la cual la presión cambiará más rápidamente. Otro ejemplo es el de considerar el mapa de líneas de nivel de una montaña como campo escalar, que asigna a cada pareja de coordenadas latitud/longitud un escalar altitud (campo escalar de 2 variables). En este caso el vector gradiente en un punto genérico indicará la dirección de máxima inclinación de la montaña. Nótese que el vector gradiente será perpendicular a las líneas de contorno (líneas "equiescalares") del mapa. El gradiente se define como el campo vectorial cuyas funciones coordenadas son las derivadas parciales del campo escalar, esto es:

${\displaystyle {\boldsymbol {\nabla }}f({\mathbf {r}})=\left({\frac {\partial f({\mathbf {r}})}{\partial x_{1}}},\dots ,{\frac {\partial f({\mathbf {r}})}{\partial x_{n}}}\right)}$

Esta definición se basa en que el gradiente permite calcular fácilmente las derivadas direccionales. Definiendo en primer lugar la derivada direccional según un vector:

${\displaystyle {\frac {\partial \phi }{\partial {\mathbf {n}}}}\equiv \lim _{\epsilon \to 0}{\frac {\phi ({\mathbf {r}}-\epsilon {\hat {\mathbf {n}}})-\phi ({\mathbf {r}})}{\epsilon }}}$

Una forma equivalente de definir el gradiente es como el único vector que, multiplicado por el vector unitario, da la derivada direccional del campo escalar:

${\displaystyle {\frac {\partial \phi }{\partial {\mathbf {n}}}}={\mathbf {n}}\cdot {\boldsymbol {\nabla }}\phi }$

Con la definición anterior, el gradiente está caracterizado de forma unívoca. El gradiente se expresa alternativamente mediante el uso del operador nabla:

${\displaystyle {\rm {grad}}\ \phi =\nabla \phi }$

Divergencia:

La divergencia de un campo vectorial mide la diferencia entre el flujo saliente y el flujo entrante de un campo vectorial sobre la superficie que rodea a un volumen de control, por tanto, si el campo tiene "fuentes" la divergencia será positiva, y si tiene "sumideros", la divergencia será negativa. La divergencia mide la rapidez neta con la que se conduce la materia al exterior de cada punto, y en el caso de ser la divergencia idénticamente igual a cero, describe al flujo incompresible del fluido. Llamado también campo solenoidal.

La divergencia de un campo vectorial en un punto es un campo escalar, y se define como el flujo del campo vectorial por unidad de volumen conforme el volumen alrededor del punto tiende a cero:

${\displaystyle {\rm {div}}{\vec {F}}=\nabla \cdot {\vec {F}}=\lim _{\Delta V\to 0}{\frac {1}{\Delta V}}\oint _{S}{\vec {F}}\cdot d{\vec {S}}}$

donde ${\displaystyle S}$ es una superficie cerrada que se reduce a un punto en el límite. El símbolo ${\displaystyle \nabla }$ representa el operador nabla.

Esta definición está directamente relacionada con el concepto de flujo del campo. Como en el caso del flujo, si la divergencia en un punto es positiva, se dice que el campo posee fuentes. Si la divergencia es negativa, se dice que tiene sumideros. El ejemplo más característico lo dan las cargas eléctricas, que dan la divergencia del campo eléctrico, siendo las cargas positivas manantiales y las negativas sumideros del campo eléctrico.

Se llaman fuentes escalares del campo ${\displaystyle {\vec {F}}}$ al campo escalar que se obtiene a partir de la divergencia de ${\displaystyle {\vec {F}}}$

${\displaystyle \rho ({\vec {r}})=\nabla \cdot {\vec {F}}({\vec {r}})}$

La divergencia de un campo vectorial se relaciona con el flujo a través del teorema de Gauss o teorema de la divergencia.

Coordenadas cartesianas

Cuando la definición de divergencia se aplica al caso de un campo expresado en coordenadas cartesianas,

el resultado es sencillo:

${\displaystyle \nabla \cdot {\vec {F}}={\frac {\partial F_{x}}{\partial x}}+{\frac {\partial F_{y}}{\partial y}}+{\frac {\partial F_{z}}{\partial z}}}$

Coordenadas ortogonales

Sin embargo, para un caso más general de coordenadas ortogonales curvilíneas, como las cilíndricas o las esféricas, la expresión se complica debido a la dependencia de los vectores de la base con la posición. La expresión para un sistema de coordenadas ortogonales es:

${\displaystyle \nabla \cdot {\vec {F}}={\frac {1}{h_{1}h_{2}h_{3}}}\left({\frac {\partial (F_{1}h_{2}h_{3})}{\partial q_{1}}}+{\frac {\partial (h_{1}F_{2}h_{3})}{\partial q_{2}}}+{\frac {\partial (h_{1}h_{2}F_{3})}{\partial q_{3}}}\right)}$

Donde los son los factores de escala del sistema de coordenadas, relacionados con la forma del tensor métrico en dicho sistema de coordenadas. Esta fórmula general, para el caso de coordenadas cartesianas (${\displaystyle h_{x}=h_{y}=h_{z}=1}$) se reduce a la expresión anterior.

Para coordenadas cilíndricas (${\displaystyle h_{\rho }=h_{z}=1,\ h_{\varphi }=\rho }$) resulta:

${\displaystyle \nabla \cdot {\vec {F}}={\frac {1}{\rho }}{\frac {\partial (\rho F_{\rho })}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial F_{\varphi }}{\partial \varphi }}+{\frac {\partial F_{z}}{\partial z}}}$

Para coordenadas esféricas)resulta

${\displaystyle \nabla \cdot {\vec {F}}={\frac {1}{r^{2}}}{\frac {\partial (r^{2}F_{r})}{\partial r}}+{\frac {1}{r{\sin }\theta }}{\frac {\partial ({\sin }\theta F_{\theta })}{\partial \theta }}+{\frac {1}{r{\sin }\theta }}{\frac {\partial (F_{\varphi })}{\partial \varphi }}}$

Coordenadas generales

En sistemas de coordenadas generales, no necesariamente ortogonales, la divergencia de un vector puede expresarse en términos de las derivadas parciales respecto a las coordenadas y el determinante del tensor métrico:

${\displaystyle \operatorname {div} \ \mathbf {v} ={\frac {1}{\sqrt {|g|}}}{\frac {\partial }{\partial x^{k}}}\left({\sqrt {|g|}}v^{k}\right)}$

Teorema de la divergencia

El teorema de la divergencia, frecuentemente llamado teorema de Gauss, relaciona el flujo de un campo vectorial a través de una superficie cerrada con la integral de la divergencia de dicho campo en el interior del volumen encerrado por una superficie. Ese resultado lo hace interesante tanto en aplicaciones relacionadas con la electrostática como en la mecánica de fluidos.

El teorema se enuncia así: Sea una función vectorial ${\displaystyle \mathbf {v} }$ diferenciable definida sobre un conjunto ${\displaystyle \Omega \subset \mathbb {R} ^{3}}$ y sea ${\displaystyle {\mathcal {R}}\subset \Omega }$ un conjunto cerrado limitado por una frontera ${\displaystyle \partial {\mathcal {R}}}$ o superficie de contorno (que sea una variedad diferenciable) y sea ${\displaystyle \mathbf {n} }$ el vector normal en cada punto de la superficie, entonces se cumple que:

 

Permitividad:

Llamada también constante dieléctrica es una constante física que describe cómo un campo eléctrico afecta y es afectado por un medio. La permitividad del vacío es 8,8541878176x10-12 C2 / Nm2.

La permitividad está determinada por la tendencia de un material a polarizarse ante la aplicación de un campo eléctrico y de esa forma anular parcialmente el campo interno del material. Está directamente relacionada con la susceptibilidad eléctrica. Por ejemplo, en un condensador una alta permitividad hace que la misma cantidad de carga eléctrica se almacene con un campo eléctrico menor y, por ende, a un potencial menor, llevando a una mayor capacidad del mismo.

Permeabilidad:

Es la capacidad que tiene un material de permitirle a un flujo que lo atraviese sin alterar su estructura interna. Se afirma que un material es permeable si deja pasar a través de él una cantidad apreciable de fluido en un tiempo dado, e impermeable si la cantidad de fluido es despreciable.

La velocidad con la que el fluido atraviesa el material depende de tres factores básicos:

• la porosidad del material y su estructura;
• la viscosidad del fluido considerado, afectada por su temperatura;
• la presión a que está sometido el fluido.

Para ser permeable, un material debe ser poroso, es decir, debe contener espacios vacíos o poros que permitan un paso fácil del fluido a través del material. A su vez, tales espacios deben estar interconectados para que el fluido disponga de caminos para pasar a través del material.

Por otro lado, hay que hablar de una "permeabilidad intrínseca" (también llamada "coeficiente de permeabilidad"); como constante ligada a las características propias o internas del terreno. Y de una "permeabilidad real" o de Darcy, como función de la permeabilidad intrínseca más las de las características del fluido.